一級建築士：崩壊荷重・不静定構造物、例題4（構造）

崩壊荷重P、1階の右側の柱に作用するQc、1階の右側の反力V、2階の梁に作用するQbを求めよ。

ただし、梁、柱の全塑性モーメントはMpとする。

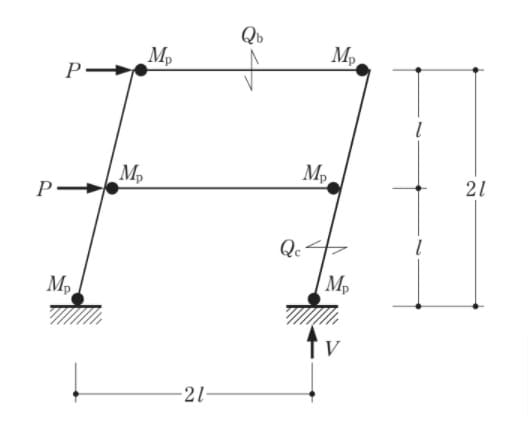
解いてみた。

①崩壊荷重を求める。

ΣMθ=ΣPδにより、崩壊荷重Pを求める。

ΣMθ=6Mpθ

ΣPδ=Pδ1（1階）+Pδ2（2階）

ここでδ1=θL、θ2=θ×2L=2θL

6Mpθ=3PθL

P=2Mp/L

②2階の梁に作用するQbを求める。

せん断力は曲げモーメントの和に対する傾きであるため

Qb=(Mp+Mp)/2L=Mp/L

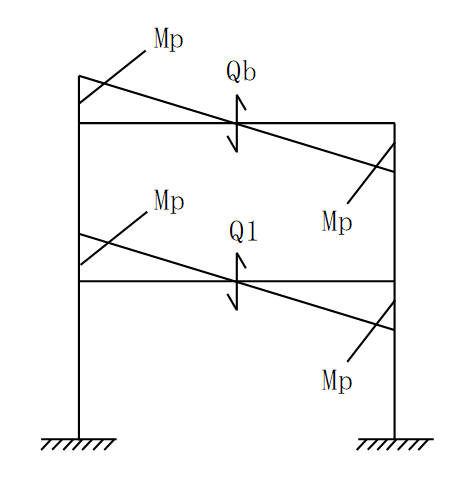
③1階の右側の柱に作用するQcを求める。

②と同様にせん断力は曲げモーメントの和に対する傾きであるため

Qc=(Mp+Mp)/2L=Mp/L

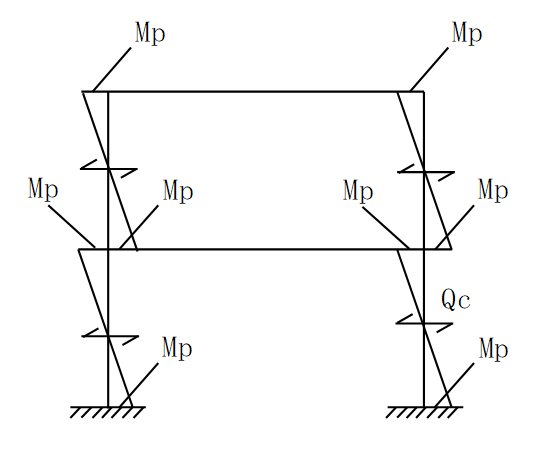
④1階の右側の反力Vを求める。

2階の梁に作用するQb=Mp/Lである。

1階の梁に作用する曲げモーメントと柱の距離が同じであるためQ1階梁もMp/Lである。

鉛直方向のつり合いから

V=(Mp/L+Mp/L)=2Mp/L