一級建築士：断面二次モーメントの大小関係、例題1（構造）

X軸、Y軸に対する断面二次モーメントの大小関係を答えよ。

解いてみた

前提条件

• 断面二次モーメントの矩形の式はI＝BH^3/12となっている。B：幅、H：高さ。
• 断面二次モーメントは全体から空洞部分を差し引いて求める、か、分割して累加して求める。
• 分割する理由は算定軸に接していない（浮いている）場合は矩形の式を用いることができないため。

定性解法（計算しないから早い）

X軸

まずはX軸に対して考えるが、この問題のように同じ高さHであれば幅Bが広いほうが大きな値となる。よってIxa=Ixb>Ixcとなることが分かる。（選択肢3・4）

Ixa=Ixbであるが、全体から差し引かれるべき軸の空洞の部分はx軸に対して同じ幅、同じ高さであるため、同じ断面二次モーメントとなる。

Y軸

90度回転して、Y軸について考える。

I＝BH^3/12に対してA、B、CはいずれもB（幅）が一定の8aであり、高さHが異なる。

Cのみ高さBが小さいので、選択肢4が除かれIya>Iyb>Iycとなることが分かる。

余談、と言いながらかなり重要

ぶっちゃけ式(I=BH^3/12)の形で感覚的に分かるけど、同じ断面積であれば高さが高いほど（3乗に比例）、幅が広いほど大きな数字となる。

曲げを大きく受ける上下縁のところに断面設けておけば、抵抗する耐力も大きくなるよねって考え方。

つまり、H型とかロ型の空洞を設けたほうが断面二次モーメントが大きく取れるよねって話。

もっと言うとH型は90度回転させると上下縁に断面がなく、曲げをあまり受けない中央部に断面があって構造上不利になるので、ロ型が一番構造合理性が高い。

まとめるとこういう問題の類はロ型>H型>■型となることを覚えておけばかなり役に立つ。

定量解法（きっちり計算して比較）

X軸

Ixa=Ixb=BH^3/12-B'H7^3/12=6a×8a^3/12-6a×4a^3/12=224a^4

Ixc=BH^3/12=4a×8a^3/12≒171a^4

X軸結果

Ixa=Ixb(225a^4)>Ixc(171a^4)

Y軸

Iya=BH^3/12-B'H'^3/12=8a×6a^3/12-4a×4a^3/12≒122a^4

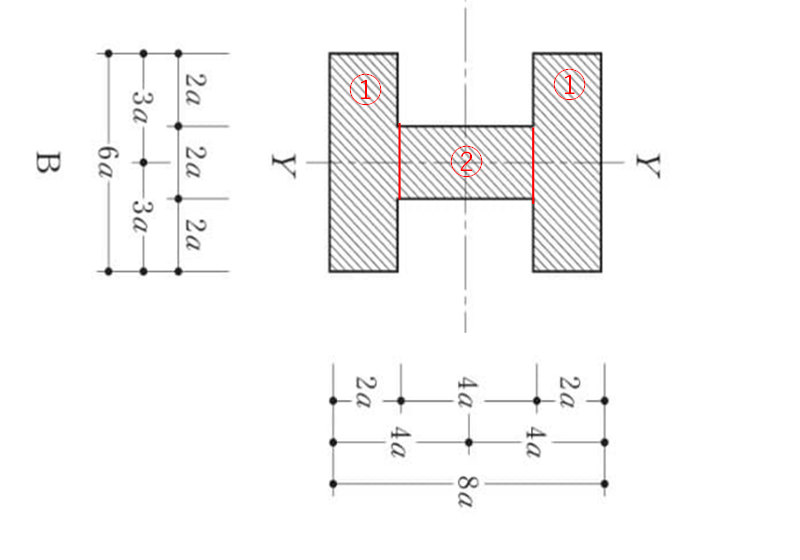
全体-中空で計算することもできるけど、Y軸に接しない場合の断面二次モーメントの公式を覚えるのめんどうなので、Y軸にすべて接する形で分割・累加して計算する。

Iyb=2×B1H1^3/12+B2H2^3/12

=2×2a×6a^3/12+4a×2a^3/12≒74a^4

Iyc=BH^3/12=8a×4a^3/12=42a^4

y軸結果

Ixa(122a^4)>Ixb(74a^4)>Ixc(42a^4)